EEE 51 Tutorial 3

The DC response of a simple common-emitter amplifier

In tutorial 2, we obtained the ideal BJT parameters of the 2N2222A transistor. We can now use this transistor to build more complex circuits like amplifiers. Let us start with a simple common emitter amplifier, shown below:

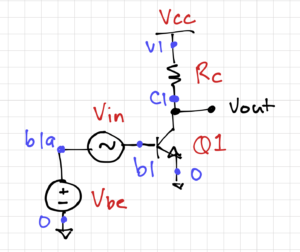
Figure 1: A common emitter amplifier.

The SPICE netlist is given below. Let’s save this as ‘amplifier_ce.sp‘.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
* Common Emitter Amplifiers
* LPA 2020-04-18
 
.include 2N2222A.lib
.options savecurrents
 
Q1      c1 b1 0 Q2n2222a
Rc      v1 c1   2.5k
Vcc     v1 0    dc 5
Vin     b1 b1a  dc 0 sin(0 10m 1k)
Vbe     b1a 0   dc 682.73m
 
.control
 
dc Vin -100m 100m 1m
wrdata ce_amp_transfer_sim.dat v(c1) @Q1[ic]
 
tran 1u 5m
wrdata ce_amp_transient_sim.dat v(b1) v(c1)
 
.endc
 
.end

If we want to bias the transistor at a collector current of 1mA, we can use our results in the previous tutorials, and set $V_{BE}=682.73\mathrm{mV}$. Recall that by writing a KVL equation at the output:

$V_{CC}-I_C\cdot R = V_{CE}$

Thus, for $V_{CC}=5\mathrm{V}$ and $I_C=1\mathrm{mA}$, we need a resistor $R_c=2.5\mathrm{k\Omega}$ to give us a $V_{CE}=2.5\mathrm{V}$. Note that choosing $V_{CE}=\tfrac{1}{2}V_{CC}$, we maximize the output swing of the amplifier.

Also note that the total base voltage is:

$v_{BE}=$ Vbe + Vin

Let’s look at the first analysis in the control portion of the netlist: the DC analysis. By sweeping Vin, we are merely sweeping the value of the base voltage 100mV below 682.73mV (582.73mV) to 100mV above it (782.73mV).

Thus, if we start sweeping Vin, we should see an exponential increase in $I_C$, and an exponential decrease in $V_{CE}$, and hence the output voltage:

$V_{CC}-I_S\cdot e^{\frac{V{BE}}{n\cdot V_T}}\cdot R = V_{CE}=V_{OUT}$

Let’s use the following Python script to run the simulation, and plot the amplifier output voltage and the BJT’s collector current:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
import matplotlib.pyplot as plt
import numpy as np
import eee51, g51
 
# load constants
g51.init_global_constants()
 
# run ngspice
cfg = {
        'spice' : '/Applications/ngspice/bin/ngspice',
        'cir_dir' : '/Users/louis/Documents/UPEEEI/Classes/EEE 51/Mini Projects/',
        'cir_file' : 'amplifier_ce.sp',
        'transfer_data' : 'ce_amp_transfer_sim.dat'
        }
 
# note: you can do this from the command line and just process the data files
# this was done here for convenience
eee51.run_spice(cfg)
 
# open the transfer characteristics data file and get the data
vin = []    # declare list for vin
vout = []   # declare a list for vout
ic = []     # declare a list for ic
 
with open(cfg['transfer_data'], 'r') as f:
    for line in f:
        vin.append(float(line.split()[0]))
        vout.append(float(line.split()[1]))
        ic.append(float(line.split()[3]))
         
bjt_n = 1.2610858394025979
reqd_vbe = 682.73e-3
Rc = 2.5e3
g51.update_bjt_VA(-15.550605626760145)
 
index, vin_sim = eee51.find_in_data(vin, 0.0)
vo_dc = vout[index]
 
 
# define the plot parameters
plt_cfg = {
        'grid_linestyle' : 'dotted',
        'title' : r'Common Emitter Amplifier DC Transfer Curve',
        'xlabel' : r'$v_{in}$ [mV]',
        'ylabel' : r'$v_{out}$ [V]',
        'legend_loc' : 'upper left',
        'add_legend' : True,
        'legend_title' : None
        }
 
# plot the amplifier transfer characteristics
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(eee51.scale_vec(vin, g51.milli), vout, '--', \
    label = r'$v_{OUT}$ with $R_C=$2.5 k$\Omega$')
 
ax2 = ax.twinx()
ax2.set_ylabel(r'$I_C$ [mA]')
ax2.plot(eee51.scale_vec(vin, g51.milli), eee51.scale_vec(ic, g51.milli), \
         ':', color='orangered', label = r'$I_C$')
ax2.legend(loc='upper right')
 
 
eee51.add_vline_text(ax, 0, 0, r'$V_{BE}$ = ' + \
    '{:.1f}mV'.format(reqd_vbe/g51.milli))
 
eee51.add_hline_text(ax, vo_dc, -75, \
    r'$V_{OUT}=$' + '{:.2f}V'.format(vo_dc))
 
eee51.label_plot(plt_cfg, fig, ax)
plt.savefig('2N2222A_ce_transfer.png')

This produces the following graph:

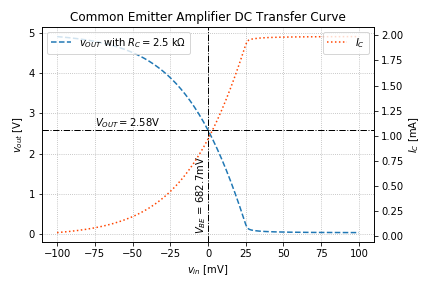
Figure 2: The DC transfer characteristics of the common emitter amplifier.

As expected, $I_C$ and $V_{OUT}$ are exponential. Also, note that the current saturates to just below 2mA, again as expected, since $V_{CE,\min}=V_{CE,sat}\approx 200\mathrm{mV}$.

$I_{C,\max}=\frac{V_{CC} - V_{CE,sat}}{R_c}\approx \frac{5\mathrm{V}-0.2\mathrm{V}}{2.5\mathrm{k\Omega}}=1.92\mathrm{mA}$

We do incur a small error. Since our output voltage is 2.58V instead of 2.5V. This means that our collector current is slightly lower than 1mA. The significance of this error will depend on the application where this amplifier will be used. The key idea here is that we know exactly how to adjust $V_{BE}$ if we really need to be very accurate.

From amplifier transfer characteristic in Figure 1, we can see that a small change in the input voltage produces a large change in the output. Thus, we can estimate the small signal gain of the amplifier as:

$A_v=\frac{\partial V_{OUT}}{\partial V_{IN}}$

Given the ideal BJT parameters, we can also estimate the gain of the amplifier using small signal analysis:

$g_m=\frac{I_C}{n\cdot V_T}$

$r_o=\frac{V_A}{I_C}$

$r_\pi=\frac{\beta}{g_m}$

Thus:

$A_v=-g_m\cdot \left(r_o\|R_c\right)$

Numerically calculating the derivative of the transfer function, and using the small signal parameters to estimate the gain:

73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
# get the gain via the slope of the transfer curve
gain_ss = np.diff(vout)/np.diff(vin)
 
ro_calc = abs(g51.bjt_VA) / ic[index]
 
gm_calc = ic[index]/(bjt_n * g51.VT)
gain_calc = -gm_calc * eee51.r_parallel([Rc, ro_calc])
 
# define the plot parameters
plt_cfg = {
        'grid_linestyle' : 'dotted',
        'title' : r'Common Emitter Amplifier Small Signal Gain',
        'xlabel' : r'$v_{in}$ [mV]',
        'ylabel' : r'Gain $A_v = \frac{\partial v_{out}}{\partial v_{in}}$',
        'legend_loc' : 'upper left',
        'add_legend' : True,
        'legend_title' : None
        }
 
# plot the amplifier transfer characteristics
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(eee51.scale_vec(vin[1:], g51.milli), gain_ss, '--', \
    label = r'$v_{OUT}$ with $R_C=$2.5 k$\Omega$')
 
eee51.add_vline_text(ax, 0, -50, r'$V_{BE}$ = ' + \
    '{:.1f}mV'.format(reqd_vbe/g51.milli))
 
eee51.add_hline_text(ax, gain_ss[index-1], -75, \
    r'$A_v=${:.2f}V'.format(gain_ss[index-1]))
 
ax.text(-100, -100, r'$g_m =\frac{I_C}{n\cdot V_T}=$' + \
    '{:.2f} mS'.format(gm_calc/g51.milli))
 
ax.text(-100, -110, r'$a_v=-g_m \cdot (R_c||r_o)=${:.2f}'.format(gain_calc))
 
eee51.label_plot(plt_cfg, fig, ax)
plt.savefig('2N2222A_ce_gain.png')

We then get the following results:

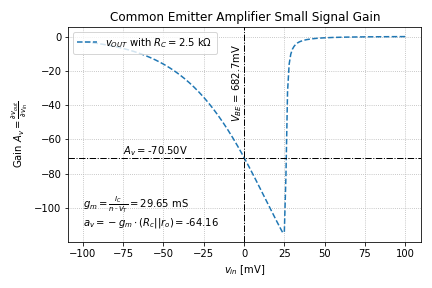
Figure 3: The common emitter small signal gain.

There is a very good agreement between the simulated gain and the gain predicted by our ideal BJT models. Notice that the gain is not constant, and depends on the value of the input voltage, but the variation is small if the inputs are “small”.

It is important to note that since our hand analysis uses relatively simple models, we do not expect the resulting values to be exactly the same as our simulation results. In fact, we can get as much as 20% errors in some cases. This is normal. Again, the crucial concept here is that we understand the relationships between the various parameters, such that we can adjust our design and/or analysis accordingly.

End of Tutorial 3

Congratulations! You have just plotted the DC transfer characteristics of a simple common emitter amplifier and obtained its small signal gain.