EEE 51 Tutorial 2D

BJT Small Signal Parameters

So far in tutorial 2, we have obtained the transistor parameters:

  • The Early Voltage, $V_A$ (tutorial 2A)
  • Saturation current, $I_S$ (tutorial 2B)
  • Ideality factor or emission coefficient of the base-emitter junction, $n$ (tutorial 2B)
  • The forward current gain, $\beta_{DC}$ (tutorial 2C)

Having these parameters will enable us to calculate the small signal equivalent circuit of the BJT.

Transistor Transconductance

We can obtain the transistor transconductance from the transistor transfer characteristics:

$g_m=\frac{\partial I_C}{\partial V_{BE}}$

We will once again use the netlist below as circuit3.sp, and again, we are going to use the data file ‘bjt_transfer_sim.dat‘.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
* Transistor Characteristic Curves
* LPA 2020-04-16
 
.include 2N2222A.lib
.options savecurrents
 
Q1      c1 b1 0     Q2n2222a
Vbe     b1 0        dc 0
Vce     c1 0        dc 0.2
 
Q2      c2 b1 0     Q2n2222a
Vce2        c2 0        dc 2.5
 
.control
 
dc Vbe 500m 750m 1m
wrdata bjt_transfer_sim.dat @Q1[ic] @Q2[ic] @Q2[ib]
 
dc Vce 30m 5 10m Vbe 0.65 0.7 0.01
wrdata bjt_output_sim.dat @Q1[ic]
  
.endc
 
.end

Let’s use the following Python script to run the simulation, read the results, and plot the transfer characteristics of the BJT.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
import matplotlib.pyplot as plt
import numpy as np
from si_prefix import si_format
import eee51, g51
 
# load constants
g51.init_global_constants()
 
specs = {
        'ic' : 1e-3,
        'vce' : 2.5
        }
     
# run ngspice
cfg = {
        'spice' : '/Applications/ngspice/bin/ngspice',
        'cir_dir' : '/Users/louis/Documents/UPEEEI/Classes/EEE 51/Mini Projects/',
        'cir_file' : 'circuit3.sp',
        'transfer_data' : 'bjt_transfer_sim.dat',
        'output_data' : 'bjt_output_sim.dat'
        }
 
# note: you can do this from the command line and just process the data files
# this was done here for convenience
eee51.run_spice(cfg)
 
# open the transfer characteristics data file and get the data
vbe = []    # declare list for vbe
ic = []     # declare a list for ic with vce = vce,sat = 0.2V
ic2 = []    # declare a list for ic with vce = 2.5V
ib2 = []    # declare a list for ib with vce = 2.5V
             
with open(cfg['transfer_data'], 'r') as f:
    for line in f:
        vbe.append(float(line.split()[0]))
        ic.append(float(line.split()[1]))
        ic2.append(float(line.split()[3]))
        ib2.append(float(line.split()[5]))
 
# convert to mV and mA
ic_mA = eee51.scale_vec(ic, g51.milli)
vbe_mV = eee51.scale_vec(vbe, g51.milli)
 
bjt_beta = [a/b for a, b in zip(ic2, ib2)]
 
# bjt parameters from our dc characterization
bjt_Is = 6.924988420125876e-13
bjt_n = 1.2610858394025979
g51.update_bjt_VA(-15.550605626760145)
g51.update_bjt_vce(specs['vce'])    
     
 
# calculate the vbe needed for vce = 2.5V
reqd_vbe = eee51.bjt_find_vbe(specs['ic'], specs['vce'], \
        bjt_Is, bjt_n, g51.bjt_VA)
 
# generate the ic for the ideal bjt model
# using our values for Is, n, and VA at vce = 2.5V
 
ic_ideal = [eee51.ideal_bjt_transfer(v, bjt_Is, bjt_n) for v in vbe]
ic_ideal_mA = eee51.scale_vec(ic_ideal, g51.milli)
 
# define the plot parameters
plt_cfg = {
        'grid_linestyle' : 'dotted',
        'title' : 'BJT 2N2222A Transfer Characteristics',
        'xlabel' : r'$V_{BE}$ [V]',
        'ylabel' : r'$I_C$ [mA]',
        'legend_loc' : 'upper left',
        'add_legend' : True,
        'legend_title' : None
        }
 
# plot the transfer characteristics at 2.5V
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(vbe_mV, eee51.scale_vec(ic2, g51.milli), '--', \
    label = 'simulation ($V_{CE}$=2.5V)')
ax.plot(vbe_mV, ic_ideal_mA, \
    label = 'ideal BJT using $I_S$=' + \
    si_format(bjt_Is, precision=2) + r'A, $n$={:.2f}, and '.format(bjt_n) + \
    r'$|V_A|$={:.2f}'.format(abs(g51.bjt_VA)))
 
eee51.add_vline_text(ax, reqd_vbe/g51.milli, 2.5, '$V_{BE}$ = ' + \
    '{:.1f}mV'.format(reqd_vbe/g51.milli))
 
eee51.add_hline_text(ax, specs['ic']/g51.milli, 550, \
    '$I_C$ = {:.1f}mA'.format(specs['ic']/g51.milli))
 
eee51.label_plot(plt_cfg, fig, ax)
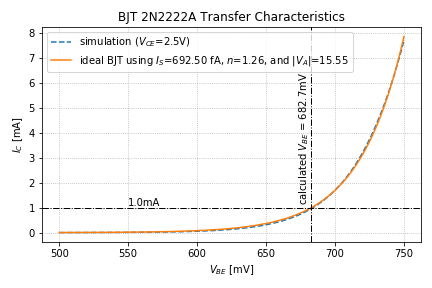
Figure 1: The BJT Transfer Characteristics.

We then take the derivative of the transfer function, as well as calculate the transconductance from the ideal BJT equation:

$g_m=\frac{I_C}{n\cdot V_T}$

Note that we can already calculate the remaining small signal parameters from the BJT parameters we have obtained:

$r_o=\frac{\left|V_A\right|}{I_C}$

$r_{\pi}=\frac{\beta}{g_m}=\frac{\beta \cdot n \cdot V_T}{I_C}$

92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
# get the derivative of ic with respect to vbe
dic2 = np.diff(ic2)/np.diff(vbe)
dic_ideal = np.diff(ic_ideal)/np.diff(vbe)
 
index, vbe_sim = eee51.find_in_data(vbe, reqd_vbe)
gm_sim = dic2[index-1]
gm_ideal = dic_ideal[index-1]
 
# calculate the bjt small signal parameters
gm_calc = ic2[index]/(bjt_n * g51.VT)
 
ro_calc = abs(g51.bjt_VA) / ic2[index]
rpi_calc = bjt_beta[index] / gm_calc
 
ao_calc = gm_calc * ro_calc
 
# define the plot parameters
plt_cfg = {
        'grid_linestyle' : 'dotted',
        'title' : r'BJT 2N2222A ${\partial I_C}/{\partial V_{BE}}$',
        'xlabel' : r'$V_{BE}$ [V]',
        'ylabel' : r'${\partial I_C}/{\partial V_{BE}}$ [mS]',
        'legend_loc' : 'upper left',
        'add_legend' : True,
        'legend_title' : None
        }
 
# plot the derivative of transfer characteristics at 2.5V
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(vbe_mV[1:], eee51.scale_vec(dic2, g51.milli), '--', \
    label = 'simulation ($V_{CE}$=2.5V)')
ax.plot(vbe_mV[1:], eee51.scale_vec(dic_ideal, g51.milli), \
    label = 'ideal BJT using $I_S$=' + \
    si_format(bjt_Is, precision=2) + r'A, $n$={:.2f}, and '.format(bjt_n) + \
    r'$|V_A|$={:.2f}V'.format(abs(g51.bjt_VA)))
 
eee51.add_vline_text(ax, reqd_vbe/g51.milli, 75, r'$V_{BE}$ = ' + \
    '{:.1f}mV'.format(reqd_vbe/g51.milli))
 
eee51.add_hline_text(ax, gm_sim/g51.milli, 600, \
    r'$g_m$ = {:.2f}mS (sim)'.format(gm_sim/g51.milli))
 
ax.text(500, 175, r'$|V_A|$={:.2f}V, '.format(abs(g51.bjt_VA)) + \
        r'$\beta_{DC}=$' + '{:.2f}'.format(bjt_beta[index]) )
ax.text(500, 150, r'$g_{m,ideal}$' + '={:.2f} mS'.format(gm_ideal/g51.milli))
 
ax.text(500, 125, r'$g_m=\frac{I_C}{n \cdot V_T}=$' + \
        '{:.2f} mS'.format(gm_calc/g51.milli))
 
ax.text(500, 100, r'$r_o=\frac{|V_A|}{I_C}=$' + \
        si_format(ro_calc, precision=2) + '$\Omega$')
 
ax.text(580, 100, r'$r_\pi=\frac{\beta_{DC}}{g_m}=$' + \
        si_format(rpi_calc, precision=2) + '$\Omega$')
 
ax.text(500, 75, r'$a_o=|g_m \cdot r_o|=${:.2f}'.format(ao_calc))
 
eee51.label_plot(plt_cfg, fig, ax)
plt.savefig('2N2222A_small_signal_2500mV.png')

We end up with the small signal parameters of the 2N2222A for $I_C=1\mathrm{mA}$ and $V_{CE}=2.5\mathrm{V}$:

Figure 2: The transconductance plot of the 2N2222A BJT and the derived small signal BJT parameters.

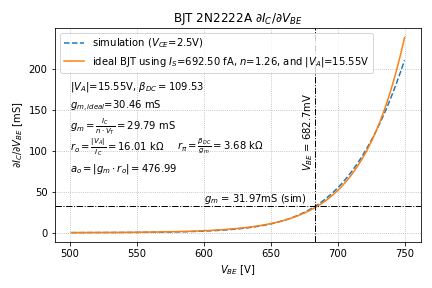
Notice that the difference between the simulation data and the ideal BJT model is much more pronounced. Since the small signal parameters depend on the derivatives of the transistor characteristics, the matching between the first derivatives must also be taken into account.

It is very important to remember that the small signal BJT parameters change with the bias current.

End of Tutorial 2D

Congratulations! You have just derived the BJT small signal model parameters from the transistor characteristics.